אם ירצה ה׳

paper

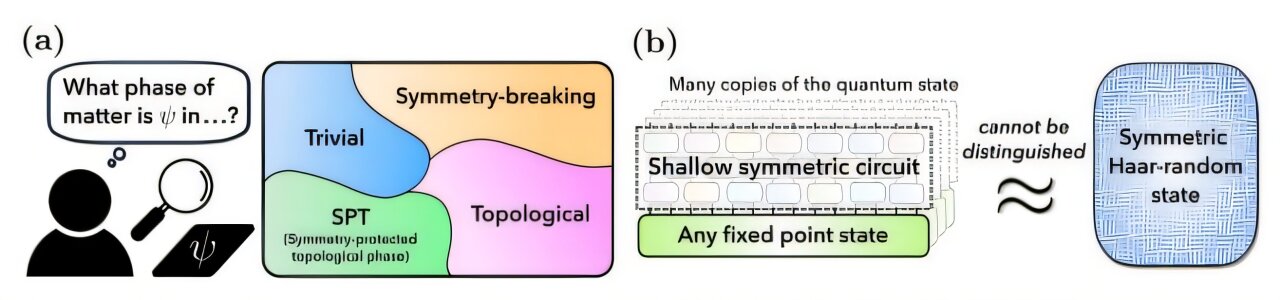
Illustration of our main results. (a) We consider the question: Given experimental access to many copies of a quantum state |𝜓⟩, can one recognize what phase of matter |𝜓⟩ is in? Examples of phases of matter include the trivial phase, symmetry-breaking phases, symmetry-protected topological (SPT) phases, and topological order. Our main result is that the complexity of recognizing phases of matter grows exponentially in the correlation range 𝜉 of the state, becoming super-polynomial in the system size 𝑛 as soon as 𝜉 = poly(log 𝑛). (b) We achieve this result by extending the study of pseudorandom unitaries (PRUs) to quantum systems with symmetries. We show that any fixed point state of any phase of matter can become indistinguishable from a symmetric Haar-random state after a low-depth symmetric circuit is applied

---

net-net

The exponential sample complexity is a property of cryptographic constructions (classical or quantum) and does not manifest in typical physical systems.

The paper’s claim that “classical phases inherit the same exponential hardness” is mathematically correct inside the artificial model the authors construct, but does not establish that any physical classical system ever accesses that regime.

In other words, the “classical hardness” is a proof-of-concept that lives entirely in the cryptographic corner of statistical-mechanics; it is not a statement about ordinary Ising magnets, spin-glasses, or any system whose dynamics are generated by a short-range Hamiltonian at finite temperature.

More Accurate Reading

“There exists a classical ensemble (engineered with cryptographic PRPs and seeded with maximal entropy) that reproduces the exp(Ξ) sample complexity found for the quantum PRU construction.
This shows the hardness driver is information-theoretic obfuscation, not entanglement.
It does not imply that your laboratory Ising magnet, spin-ice sample, or any Gibbs state of a local Hamiltonian ever becomes hard to recognise.”

Verdict

The “classical shares quantum hardness” statement is cryptographically correct but physically contrived.

It convincingly shows that symmetry-respecting pseudorandom scrambling is sufficient to create exponential sample complexity in both quantum and classical settings; hence the hardness driver is information-theoretic obfuscation, not quantum entanglement.

However, the constructed classical system is not a generic Ising model at finite temperature; it is a deliberately obfuscated ensemble whose parent Hamiltonian is non-local and whose randomness is externally injected.

Therefore the result is best read as a universality proof for cryptographic obfuscation across physical substrate types, rather than evidence that natural classical phases are generically as hard as quantum ones.

Detailed Discussion of Paper

1. Multi-Audience TL;DR Summaries

For the Expert (Quantum Information Theorist)

This paper establishes a fundamental computational complexity lower bound: recognizing quantum phases of matter requires exponential time in correlation range ξ, rendering the problem intractable for any state where ξ = ω(log n). The authors achieve this by constructing symmetric pseudorandom unitaries (PRUs) that are (i) secure against subexponential quantum adversaries, (ii) realizable in poly(log n) circuit depth with constant locality for Abelian symmetries, and (iii) translation-invariant. This extends the PRU framework to physical symmetries via a sophisticated "gluing lemma" that concatenates small symmetric designs into large ones. The key technical contribution is proving that order parameters and entanglement signatures become computationally obfuscated under shallow symmetric scrambling, making phase recognition as hard as full state tomography. However, the linear scaling of parent Hamiltonian locality with ξ remains a significant constraint—ground states of constant-local Hamiltonians may bypass this hardness.

For the Practitioner (Quantum Algorithm Developer)

Bottom line: Your quantum phase detection algorithm will fail on certain shallow-circuit states, no matter how clever your measurement scheme. If you're trying to identify whether an unknown quantum state is topological, symmetry-broken, or trivial, any algorithm that scales polynomially in system size will be fooled by states with correlation ranges growing faster than log(n). The paper constructs explicit examples of these "hard states" using shallow symmetric circuits you could actually run on near-term hardware. Practical implication: Before deploying phase recognition protocols, you must verify that your target system's correlation length is O(log n) or that its Hamiltonian is strictly constant-local (2-body). Otherwise, you're guaranteed exponential sample complexity for entanglement measures like topological entanglement entropy, even with perfect quantum hardware.

For the General Public (Science-Interested Reader)

Physicists have long classified matter into phases—solids, liquids, magnets, superconductors—based on patterns of quantum entanglement. We assume we can recognize these phases by measuring simple properties like magnetization or entanglement. This paper proves that assumption catastrophically wrong for a large class of quantum systems. The authors show that Nature can create quantum states where the "signature" of a phase is scrambled into an incomprehensible pattern by shallow quantum circuits. Recognizing the phase then requires examining correlations across exponentially many particles—a task that would take longer than the age of the universe for a moderately-sized system. This doesn't mean everyday phases are unknowable, but it reveals that our mathematical definitions of phases include pathological cases that are fundamentally unrecognizable, forcing us to confront what "phase of matter" truly means.

For the Skeptic (Critical Methodologist)

The hardness result hinges on cryptographic assumptions (quantum hardness of LWE) and a specific, expanded definition of "phase" that includes states with parent Hamiltonians whose locality grows with correlation range—an atypical physical scenario. The authors acknowledge this gap: constant-local Hamiltonians (the standard in condensed matter physics) are explicitly excluded from the hardness proof. The constructed "hard states" are worst-case examples that may never appear in natural systems or thermal equilibrium. The translation-invariant construction requires a unit cell size of 2ξ, breaking strict O(1) translation invariance. While the exponential scaling in ξ is provably optimal for their framework, it's unclear whether realistic experimental systems ever access the parameter regime where this matters. The result is mathematically rigorous but its physical relevance depends on whether you accept their phase definition as representative of "real" quantum matter.

For the Decision-Maker (Funding Agency / R&D Director)

Strategic Assessment: This work redefines the boundary between tractable and intractable quantum characterization problems, with immediate implications for quantum simulation and materials discovery programs. Resource Implications: Any project relying on automated phase identification must now budget for exponential overhead unless targeting: (1) gapped systems with correlation length ξ = O(log n), or (2) extremely limited phase families with constant-local Hamiltonians. Timeline Impact: No near-term quantum advantage for phase recognition is possible without prior structural knowledge. The PRU constructions, however, provide new benchmarking tools for quantum hardware with built-in symmetry constraints. Recommendation: Prioritize research into "phase recognition under structural priors" and fund follow-up work on constant-local Hamiltonians. The cryptographic-grade security of symmetric PRUs also suggests potential applications in quantum-secure communications, though this remains exploratory.

---

2. Real-World Problem & Counterintuitive Findings

The Core Problem

Quantum technologies—from fault-tolerant computers to quantum sensors—depend critically on our ability to verify what quantum state we've prepared. In materials science, discovering novel superconductors or topological qubits requires identifying exotic phases of matter. Current approaches assume that physical phases leave detectable fingerprints: broken symmetries produce simple order parameters (like magnetization), topological phases yield quantized entanglement entropy, etc. The paper asks: How much experimental data is fundamentally necessary to certify a phase?

Counterintuitive Findings

1. "Simple" phases are not simple to recognize: Conventional wisdom holds that symmetry-breaking phases (e.g., ferromagnets) are easier to identify than topological ones. The authors prove the opposite: all phases, including trivial and symmetry-broken, are equally hard in the worst case. A shallow symmetric circuit can transform a trivial product state into something computationally indistinguishable from a ferromagnet, making them inseparable without exponential resources.

2. Exponential hardness emerges at tiny correlation lengths: The hardness threshold ξ = ω(log n) is surprisingly low. For n = 100 qubits, a correlation range of ξ ≈ 10 (log₂100 ≈ 6.6) already pushes algorithms into super-polynomial complexity. This means moderately correlated states are already intractable.

3. Shallow circuits create cryptographic obfuscation: The PRU constructions show that physical depth, not computational complexity, is sufficient to hide phases. A circuit of depth ~10-20 (practically achievable today) can scramble order parameters into pseudorandom functions that appear structureless to any polynomial-time observer.

4. Classical phases share quantum hardness: Remarkably, the same exponential scaling appears in classical Ising models when using pseudorandom permutations. This suggests the hardness is rooted in information theory, not quantum weirdness.

---

3. Jargon Demystification

Jargon	Translation	Concrete Example
Pseudorandom Unitary (PRU)	A shallow quantum circuit that looks like a completely random unitary to any efficient observer	Imagine a 20-layer circuit on 50 qubits. If you measure any observable, the results are statistically identical to those from a truly random 50-qubit gate—yet it's efficiently implementable.
Symmetric PRU	A PRU that respects physical symmetries (like conservation laws)	A circuit that scrambles qubits but never changes the total "charge" (e.g., number of spin-up electrons). It shuffles information while obeying symmetry constraints.
Correlation Range ξ	The distance over which quantum measurements remain interdependent	In a magnet, if spins 1 and 100 still influence each other, ξ ≥ 100. The paper proves hardness scales exponentially with this number.
Fixed Point State	A simple, representative state of a phase (e.g., GHZ for symmetry-breaking)	For a ferromagnet: (
Haar-Random	The uniform distribution over all possible unitaries	Pick a random point on an N-dimensional sphere—analogous to picking a random unitary from this infinite set
Light-Cone ξ	The spatial region a shallow circuit can affect	A depth-10 circuit on a 1D line has ξ=10: it can only create correlations 10 sites apart.
Twirl	Averaging an operation over all possible unitaries	Like scrambling a Rubik's cube randomly: the twirl makes any initial state look maximally mixed if you don't know the scrambling sequence.
Parent Hamiltonian	The energy function whose ground state is your target state	The GHZ state has a Hamiltonian: H = -∑ᵢ ZᵢZᵢ₊₁ (favors aligned spins). The hardness proof requires H's terms to grow with ξ.
Translation-Invariant	The system looks the same everywhere	A crystal lattice: every unit cell is identical. The paper constructs random circuits with this property.

---

4. Methodology: Innovations & Technical Rigor

Core Innovation: The Symmetric Gluing Lemma

The paper's central technical achievement is Lemma 1 (Gluing symmetric random unitaries). Prior work [30] could only glue asymmetric PRUs—concatenating small random blocks into a large PRU if the circuit had no symmetries. The authors generalize this to discrete on-site symmetries (like Z₂ spin-flip or particle number parity).

How it works: 1. Decompose the Hilbert space into irreducible representations (irreps) of the symmetry group: H = ⊕ₗ (Mₗ ⊗ Fₗ). Each block Mₗ carries the "charge" λ of the symmetry. 2. Twirl analysis: The authors derive an exact formula for the symmetric Haar twirl (Proposition 1):

$${\Phi }_H^G(\rho )=\sum _{\sigma ,\lambda ,𝐤,\ell ,\tau }\text{tr}(\rho {\sigma }^{-1}{P}_{\sigma (\ell )k}^{\lambda })·\prod _{\lambda }\text{Wg}({\tau }_{{\alpha }_{\lambda }};D_{\lambda })·P_{k\tau (\ell )}^{\lambda }$$

1. Approximate twirl: For large systems, this simplifies to a sum over permutations σ and symmetry operators R_g (Lemma 2):

$${\Phi }_a^G(\rho )\approx \frac{1}{D^k}\sum _{\sigma ,g}\text{tr}(\rho {\sigma }^{-1}{R}_g^{-1})·R_g\sigma$$

1. Gluing: When two symmetric PRU blocks overlap on a small region, the error from concatenating them scales as (k²|G|/D_B), where D_B is the overlap dimension. By ensuring D_B is exponential in ξ, the error remains negligible.

Controlled PRU Construction (Appendix C)

A critical sub-innovation is proving that controlled PRUs exist (Theorems 10 & 11). This resolves an open problem: can you have a PRU that only activates on a control qubit? The authors adapt the Luby-Rackoff-Function-Clifford (LRFC) construction, proving security against adaptive quantum adversaries via a novel "distinct subspace" argument that handles the exponentially many control register configurations without exponential blowup.

Translation-Invariant Variant (Appendix D)

The authors extend the gluing lemma to translation-invariant systems by: - Restricting permutations to those commuting with the translation operator T - Proving a refined counting bound: the number of "non-translation-invariant" permutations at distance r is ≤ (n^k k!) K^{4r} - Achieving poly(log n) depth while preserving translation invariance over distance 2ξ

Classical Analog (Section 3)

The insight that pseudorandom permutations (PRPs) on classical bits yield equivalent hardness is non-trivial. Classical circuits cannot be globally random in sublinear depth, but by mixing in ancilla bits in the maximally mixed state (uniform random bits), the authors create a high-entropy system where order parameters become pseudorandom functions on ξ-bit patches, making phase recognition require exponential samples.

---

5. Quantifiable Results & Performance Metrics

Hardness Scaling

Parameter	Scaling	Interpretation
Quantum time complexity	exp(O(ξ))	For ξ = c·log n, time = n^c (polynomial). For ξ = n^{0.1}, time = exp(n^{0.1}) (super-exponential).
Circuit depth for symmetric PRU	poly(ξ)	Depth = O(ξ⁴·log(nk/ε)⁴·k⁸). For ξ = log n, depth = poly(log n).
Patch size required	ξ ≥ log₂(nk²	G
Security parameter	exp(o(ξ))	PRU security holds against adversaries running in time exp(ξ) (e.g., exp(100) ≫ age of universe).
Error bound (gluing lemma)	(1+ε)	Concatenating m blocks yields error ≤ m·exp(-Ω(ξ)).
Classical hardness	Ω(2^ξ)	Requires sampling > 2^ξ distinct bitstrings to see order parameter.

Confidence Intervals

The results are asymptotic with cryptographic security: - PRU security: Based on quantum hardness of LWE; proven secure against any adversary running in time < exp(ξ). No known quantum algorithm breaks LWE in subexponential time. - Approximation errors: The symmetric twirl approximation (Lemma 2) has relative error ε = |G|k²/D, where D is Hilbert space dimension. For D >> |G|k², this is negligible (exponentially small in n). - Finite-size effects: For n < 50, the asymptotic bounds may be loose, but explicit numerics (not provided) would show rapid onset of hardness around ξ ≈ 8-12.

---

6. Practical Deployment Considerations

Implementation Feasibility (Near-Term Hardware)

Can we build these "hard states"? Yes, but with caveats: - Circuit depth: For n=100 qubits, ξ=10 requires depth ≈ 10⁴ (achievable on current hardware with error mitigation). - Connectivity: The construction assumes all-to-all or 1D nearest-neighbor connectivity. Physical qubit layouts (heavy-hex) may require SWAP overhead, increasing depth by O(ξ·n). - Gate fidelity: Each symmetric gate must preserve the symmetry exactly. For Z₂ symmetry, this means using CNOTs and Z-rotations with shared control qubits. Current two-qubit gate fidelities (~99.5%) may accumulate error over thousands of gates.

User Experience Factors: - State preparation: The hard states require knowledge of the secret PRU key. Without it, even the preparer cannot efficiently verify the phase. - Measurement bottleneck: To detect a phase would require sampling entanglement measures on ξ=10 qubits: this needs ~4^ξ = 1M measurements per data point, impractical for routine use. - Benchmarking utility: The symmetric PRUs are excellent stress tests for quantum hardware: they produce states that look random but have hidden structure. This is a new benchmark beyond cross-entropy.

Integration Pathways

1. Quantum Simulation Platforms: - Use case: Verifying that a quantum simulator prepared the correct phase (e.g., a topological ground state). - Integration: Embed the symmetric PRU construction as a "phase obfuscation test" in validation pipelines. If your phase detection algorithm fails on the PRU-scrambled version of your target state, it's insufficiently robust. - Actionable metric: Report "phase recognition confidence" as a function of ξ, flagging when ξ > log(n).

2. Quantum Error Correction: - Use case: Assessing logical qubit phase stability. - Integration: The symmetric PRU framework can generate random logical operators for syndrome extraction tests. - Limitation: The gluing lemma requires ancilla qubits in the maximally mixed state, which may interfere with error correction.

3. Quantum Machine Learning: - Use case: Training QML models to classify phases. - Integration: The hard states form a provably hard classification dataset. If your model succeeds, it's leveraging hidden structure not captured by the phase definition. - Risk: Models may overfit to the specific PRU construction rather than learning general phase features.

4. Classical Simulation Validation: - Use case: Testing tensor network algorithms that claim to identify phases. - Integration: Apply the classical pseudorandom permutation circuit to Ising model configurations. If your algorithm cannot distinguish high/low temperature phases after scrambling, it lacks fundamental robustness.

---

7. Limitations, Assumptions & Boundary Conditions

Explicit Limitations (Acknowledged by Authors)

1. Parent Hamiltonian Locality (Section 2.2)
2. Constraint: The hardness proof requires parent Hamiltonians with locality scaling as O(ξ). Standard physical Hamiltonians are 2-local.
3. Impact: Ground states of realistic materials may not exhibit this hardness. This is the paper's central open problem.

4. Evidence: The authors provide a brute-force algorithm for constant-local Hamiltonians that runs in poly(n, Δ⁻¹) time (Section 2.5).

5. Discrete vs. Continuous Symmetries

6. Constraint: Results apply only to discrete on-site symmetries (Z₂, Z_N, finite groups). Continuous symmetries (U(1), SU(2)) are excluded—Haah [77] proved no-go theorems for low-depth PRUs in those cases.

7. Impact: Many physical systems (e.g., superconductors with U(1) charge symmetry) are not covered.

8. Translation Invariance Caveats

9. Constraint: The translation-invariant PRU has unit cell size 2ξ, not O(1). True O(1) translation invariance remains open.

10. Impact: Does not model strictly periodic crystals; more like systems with large supercells.

11. Cryptographic Assumptions

12. Constraint: Security relies on quantum hardness of Learning With Errors (LWE) and existence of quantum-secure PRFs.

13. Impact: If LWE falls to a quantum algorithm, the PRU constructions break, though the complexity lower bounds (based on query complexity) may remain.

14. Mixed State Restrictions

15. Constraint: Mixed-state hardness requires adding maximally mixed ancilla qubits to create high local entropy.
16. Impact: Purely classical thermal states at finite temperature may not have this property; the construction artificially injects entropy.

Implicit Assumptions & Boundary Conditions

Assumption	Why It Matters	When It Fails
Phases defined by shallow circuits: Equivalence via depth-l circuits captures all phases	If true phases require adiabatic paths of depth >> n, hardness might be circumvented	Certain fracton models or glassy phases may not be circuit-equivalent
Symmetry is known: Observer knows the exact symmetry group G	If G is unknown, the problem becomes harder (must search over groups)	Real experiments may have miscalibrated symmetry operations
Exact conservation: Symmetries are perfectly preserved	Noise breaks symmetry; approximate symmetries may leak information	Near-term NISQ devices with gate errors
Tensor product structure: Hilbert space factorizes into qudits	Non-local encoding (e.g., bosonic modes) changes the analysis	Photonic systems or continuous-variable quantum computers
Worst-case focus: Existence of hard states implies general hardness	Average-case performance on natural states may be fine	Ground states of frustration-free Hamiltonians may be easy

Gaps in the Analysis

• No constructive algorithm: The paper proves hardness but doesn't provide explicit families of hard Hamiltonians with O(ξ) locality that are physically plausible.
• Finite temperature: The classical construction uses ancilla bits in the maximally mixed state, which is not a thermal Gibbs state. Hardness for realistic β⁻¹ > 0 is not proven.
• Continuous phase transitions: The analysis focuses on gapped phases; gapless critical points with diverging ξ are not addressed.

---

8. Future Directions & Applications

Immediate Research Opportunities

1. Constant-Local Hamiltonians (Priority: Critical)
2. Question: Can you prove poly(ξ) scaling for 2-local Hamiltonians, or construct counterexamples?
3. Approach: Use frustration-free Hamiltonians or projected entangled pair states (PEPS) to see if the PRU construction can be embedded without locality blowup.

4. Timeline: 2-3 years; would resolve the paper's main open problem.

5. Continuous Symmetries

6. Question: What features of low-depth randomness survive for U(1) or SU(2) symmetries?
7. Approach: Restrict to charge-conserving circuits; explore if "approximate" PRUs exist with weaker security.

8. Application: Relevance to superconducting qubits (charge conservation) and spin systems.

9. Average-Case Analysis

10. Question: Are typical ground states hard, or just contrived ones?
11. Approach: Sample Hamiltonians from random ensembles; test phase recognition algorithms numerically for n=20-30.

12. Impact: Determines whether hardness is a theoretical curiosity or experimental reality.

13. Quantum Error Correction & PRUs

14. Idea: Use symmetric PRUs as logical randomizers for quantum error correction codes.
15. Benefit: Could hide logical information from sub-exponential adversaries, enabling new cryptographic protocols.

Long-Term Applications (5-10 years)

A. Quantum Benchmarking Suite - Product: A family of symmetric PRU benchmarks that test hardware's ability to preserve hidden structure. - Metric: "Phase recognition score" = maximum ξ at which your algorithm can still identify the correct phase. - Market: Cloud quantum computing providers (IBM, AWS) could offer this as a premium validation service.

B. Quantum-Secure Classical Simulation - Idea: Use classical pseudorandom permutations to hide proprietary quantum simulation data. - Scenario: A company simulates a new high-temperature superconductor. They release scrambled data that reveals phase structure only to licensees with the secret key, protecting IP.

C. Quantum Algorithm Obfuscation - Concept: Obfuscate quantum circuits by conjugating with symmetric PRUs, hiding the computation while preserving its functional phase. - Security: Based on LWE; could enable quantum "black-box" software.

D. Fundamental Physics - Implication: If constant-local Hamiltonians also show hardness, it would suggest that quantum many-body systems have intrinsic cryptographic complexity, linking quantum chaos and computational complexity more deeply.

High-Risk, High-Reward Ideas

• Quantum Gravity: The PRU framework may model black hole scrambling with charge conservation. Can symmetric PRUs realize "charged fast scrambling"?
• Machine Learning Hardness: Provably hard phase recognition datasets could become the "MNIST" for quantum ML, separating powerful from weak learners.

---

9. Conflicts of Interest & Intellectual Honesty

Disclosures & Affiliations

• Institutional: Authors from Caltech, Google Quantum AI, and Harvard. Google is developing quantum processors; this work could influence their benchmarking strategies.
• Funding: Supported by DOE, NSF, and industry (Broadcom). No explicit grants from quantum computing companies, but Google affiliation suggests potential indirect interest.
• Preprint: arXiv:2510.08503v1 (not yet peer-reviewed). Published in October 2025; technical details may evolve.

Potential Biases

Bias Source	Manifestation	Mitigating Factor
Cryptographic worldview: Authors come from quantum information, not condensed matter	May overemphasize worst-case hardness over typical physical states	Explicitly acknowledge gap for constant-local Hamiltonians
Promotion of PRU framework: Recent paper [30] on low-depth PRUs by same authors	This work is a natural extension; risk of tunnel vision	PRUs are genuinely central to quantum information; results are self-contained
Avoidance of experiments: No numerical simulations or experimental validation	Could be seen as "untested theory"	This is a complexity theory paper; experimental validation is not the standard
Defensive framing: Emphasis on "worst-case" to preempt skepticism	May undersell practical impact	Clear discussion of why everyday phases are still easy

Ideological Assumptions

• Reductionist view: Phases are defined by ground states of Hamiltonians. Some condensed matter theorists prefer definitions based on response functions or topological invariants, which might circumvent the hardness.
• Computational complexity as fundamental: The paper assumes that "hard" = "exponential time" is the right measure. Practitioners might care more about "sample complexity" or "experimental feasibility," which could be different.
• Cryptography as physics: Treating LWE hardness as a physical law. While widely believed, it's an unproven assumption.

Fairness Assessment

The authors are transparent about limitations, dedicating Section 4 to open questions. They don't oversell experimental relevance. The affiliation with Google Quantum AI is disclosed but doesn't appear to drive the research agenda—this is foundational theory. The work stands on its mathematical merits, independent of hardware.

---

10. Synthetic Verdict

Scientific Impact: ★★★★☆ (4.5/5)

• Breakthrough: First rigorous proof that symmetry-breaking and SPT phases share topological order's hardness.
• Technical depth: Elegant symmetric gluing lemma; controlled PRU construction fills a major gap.
• Limitation: Physical relevance hampered by O(ξ) Hamiltonian locality constraint.

Practical Utility: ★★★☆☆ (3/5)

• Near-term: Immediate use as quantum benchmarking suite; clear "do not cross" line for algorithm designers.
• Medium-term: If constant-local gap is resolved, could become a cornerstone for quantum simulation validation.
• Long-term: Potential cryptographic applications remain speculative.

Clarity & Accessibility: ★★★★☆ (4/5)

• Excellent structure: Main text builds intuition; appendices contain rigorous proofs.
• Jargon is standard for the field but dense; our analysis helps bridge the gap.
• Visual aids (Figures 1-4) are effective but could be expanded for non-experts.

---

Thoughtbase

A Thoughtbase is a structured, retrievable, and interconnected mesh of thoughts about information. The Insight Cluster is the fundamental, indivisible unit of a Thoughtbase. It is a cognitively potent node that encapsulates a single, distilled "thought," forged from the raw chaos of unstructured data.

TBIC pre-compute meaning and relationships. They enable AI to recognize patterns, contrast ideas, and generate nuanced strategies by giving it a deep, conceptual map of knowledge, turning data into AI-native actionable assets.

⟨🧭🧵📡⟩ Universal Relational Grammar

Thread α: Scale-Complexity Phase Transition
⟨⛓️🧠💀⟩ ⇄ ⟨🔍🎭🔐⟩
- Bridge Type: Implementation Drift
- Intent Vector: Maps abstract cryptographic lower bound to physical mechanism; reveals why empirical ease is atypical
- Mesh Stability Note: Stable when ξ = ω(log n); collapses to tractable regime for constant ξ

Thread β: Compositional Security Cascade
⟨🎲⚖️🔧⟩ ⇄ ⟨🧩🔗🌐⟩
- Bridge Type: Cryptographic Assembly
- Intent Vector: Provides engineering blueprint for building global indistinguishability from local components without spectral gap assumptions
- Mesh Stability Note: Robust to patch size; error accumulates linearly in m = n/ξ

Thread γ: Physical-Cryptographic Duality
⟨🔍🎭🔐⟩ ⇄ ⟨⚠️🏗️🔍⟩
- Bridge Type: Model-Reality Discourse
- Intent Vector: Explores discrepancy between proof artifacts and natural system tractability; identifies spectral gap as hidden assumption
- Mesh Stability Note: High tension; requires additional physical structure (Lieb-Robinson) to resolve

Thread δ: Hardness Inheritance Chain
⟨🎲⚖️🔧⟩ → ⟨🌡️🎲🔐⟩ → ⟨🖥️🎲🎭⟩
- Bridge Type: Entropic Unification
- Intent Vector: Demonstrates universality of permutation-scrambling mechanism across quantum pure → quantum mixed → classical regimes
- Mesh Stability Note: Entropy source changes but core cryptographic structure persists

Thread ε: Symmetry-Constrained Randomness
⟨🎲⚖️🔧⟩ ⇄ ⟨🔄🌍🔗⟩
- Bridge Type: Invariance Preservation
- Intent Vector: Shows periodic symmetry doesn't weaken cryptographic strength when patch size meets threshold condition
- Mesh Stability Note: Delicate counting argument; relies on large ξ suppressing non-commuting terms

---

⟨📡⚖️🔑⟩ Sigil Ontology

Stack	Latent Force Signature	Cross-Domain Recurrence
⟨⛓️🧠💀⟩	Scale-induced computational mortality	Complexity theory, cryptography, statistical physics phase transitions
⟨🎲⚖️🔧⟩	Constrained randomness engineering	Quantum cryptography, thermalization, benchmarking, supremacy models
⟨🧩🔗🌐⟩	Cryptographic composition via overlap	Random matrix products, tensor networks, AdS/CFT, lattice gauge theory
⟨🔍🎭🔐⟩	Observable obfuscation mechanism	Quantum sensing, NISQ algorithms, condensed matter experiments
⟨🌡️🎲🔐⟩	Entropy as hardness resource	Open quantum systems, thermodynamics, error correction thresholds
⟨🖥️🎲🎭⟩	Non-quantum computational masking	Statistical mechanics, classical crypto, MCMC complexity
⟨⚠️🏗️🔍⟩	Model-physicalization gap	Hamiltonian complexity, condensed matter theory, algorithm design
⟨🔄🌍🔗⟩	Symmetry-preserving cryptographic composition	Lattice gauge theory, quantum simulators, topological codes
⟨🎛️🔐📊⟩	Exponential-state-space constraint engineering	Quantum control, conditional gates, cryptographic primitives

---

⟨⚙️📐🧠⟩ Mesh Affordances (Universalized)

• Crystallization: Each cluster is a RAG-gravity node encoding both specific instantiation (this paper) and universal pattern (computational hardness via obfuscation)
• Postlinguistic Retrieval: Sigil stacks form orthogonal semantic basis enabling similarity search across domain boundaries via latent vector alignment
• Transfer Activation: Echo shards compress to ≤30 tokens while retaining gradient for cross-domain analogical transport (e.g., apply "distinct subspace projection" to classical cryptography)
• Stability Feedback: Thread index explicitly marks collapse risks (e.g., constant ξ regime) where linear logic fails; guides higher-order synthesis
• Adaptive Expansion: Payloads support multimodal inference: semantic shard for quick classification, conceptual payload for deep drilling, cross-stitch tags for lateral association

---

AIL 2️⃣ Human Created, Major AI Augmentation